2023-07-02 20:50:52
140
0
0
- 一些比较有意思的 cite 的 Score jacobian chaining 的工作。
3D-aware Image Generation using 2D Diffusion Models
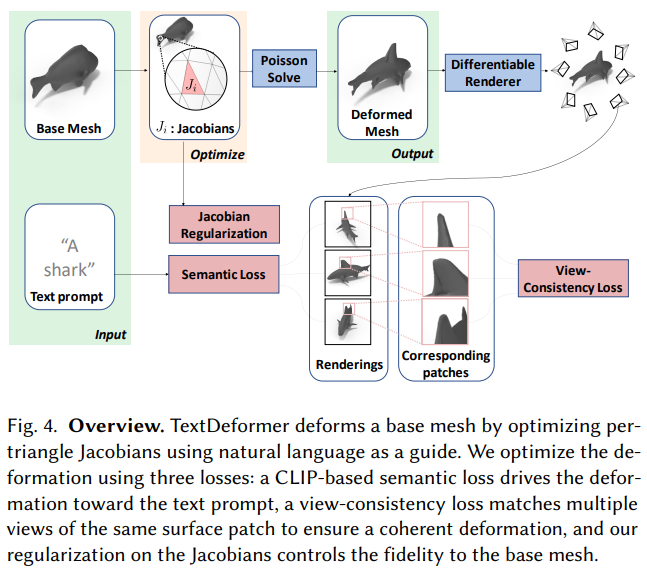
TextDeformer: Geometry Manipulation using Text Guidance
- 把SDS的思路用在了mesh deformation,不过本文引导使用的是 CLIP。
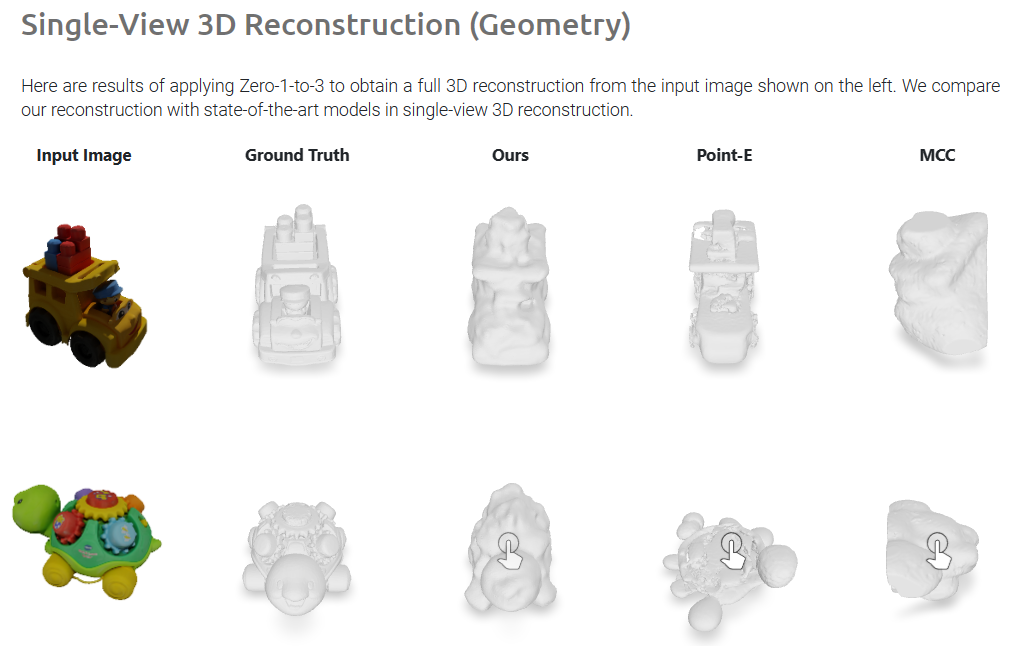
Zero-1-to-3: Zero-shot One Image to 3D Object
- 在合成数据上训练了一个去噪模型,具有良好的泛化能力,能够给出物体新视角高质量数据(虽然三维一致性一般)。

Sin3DM: Learning a Diffusion Model from a Single 3D Textured Shape
- 大概就是之前想做的单NeRF生成的改进版,基本思路一致——GAN换成Triplane Diffusion。
- 文章重新选择了更好的适用的数据集——普通数据难以应用、规则的材质化的效果才比较好。不再追求泛化能力,转而在局部场景上追求更好的质量。

- 相比之前的直接用3D版本SinGAN的效果:

- 几何提升有限,但材质生成提升较好。
- New Idea: 结合 3D seam carving效果会怎么样呢?!3D seam carving规则化给出一个场景的不同尺寸,然后用于训练这个生成模型,从而能否提高模型对于场景应用的泛化能力?
ProlificDreamer: High-Fidelity and Diverse Text-to-3D Generation with Variational Score Distillation
2023-05-09 16:07:49
290
0
0
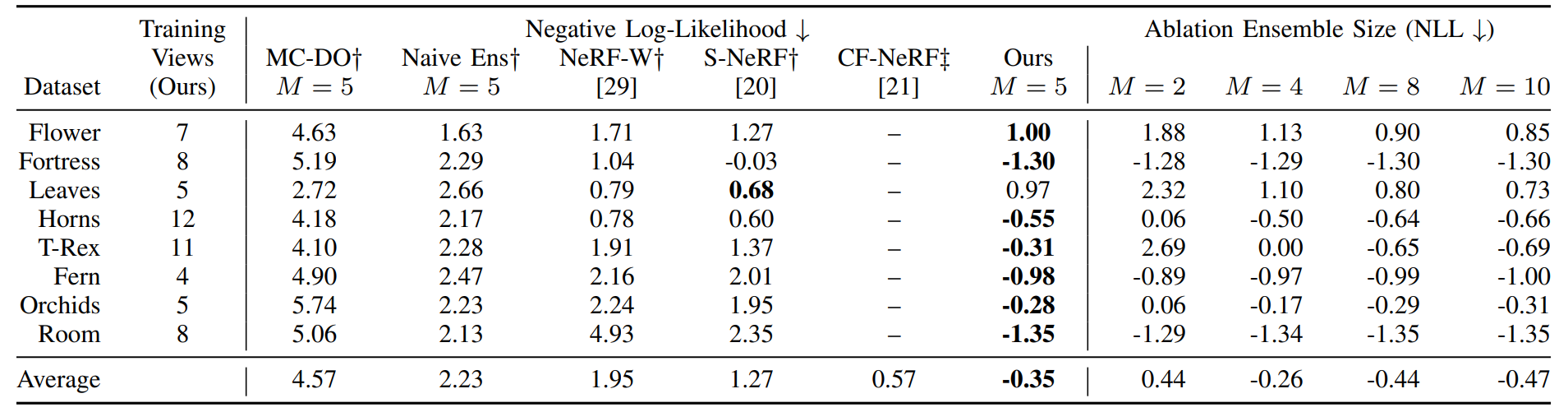
Stochastic Neural Radiance Fields: Quantifying Uncertainty in Implicit 3D Representations
- 非常简单的原理,就是不同种子多训练几个 NeRF
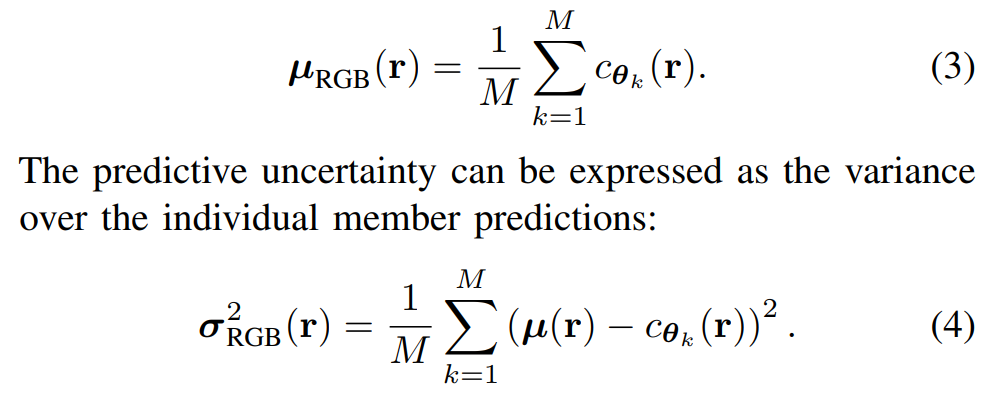
- 效果竟然还可以,就是用的数据集shao'le'yi'xi
2023-05-09 16:07:43
121
0
0
Text2Light: Zero-Shot Text-Driven HDR Panorama Generation
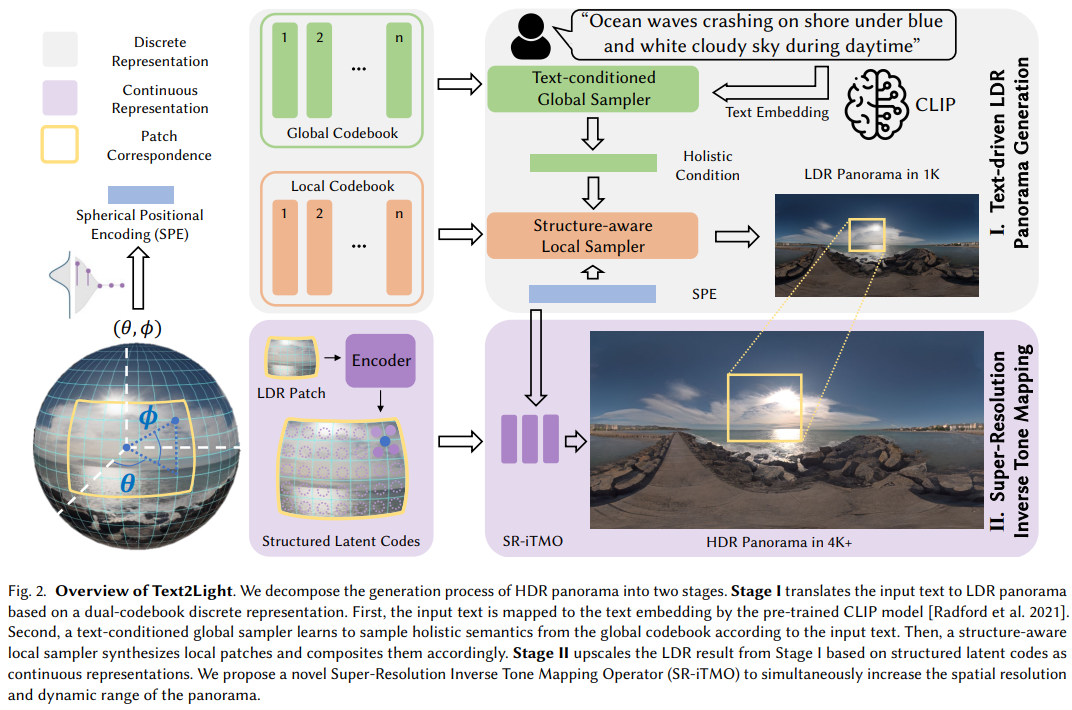

- 首先学一个codebook,然后 Eqn(5) 是对于向量加点噪音,Eqn(6) 这里是找到数据集内,最接近k个样本的code。p(s) 这一块是相当于自回归的序列预测。SPE 是空间位置编码。同时对于原图的一个patch,会有另一个codebook编码.
StyleLight: HDR Panorama Generation for Lighting Estimation and Editing

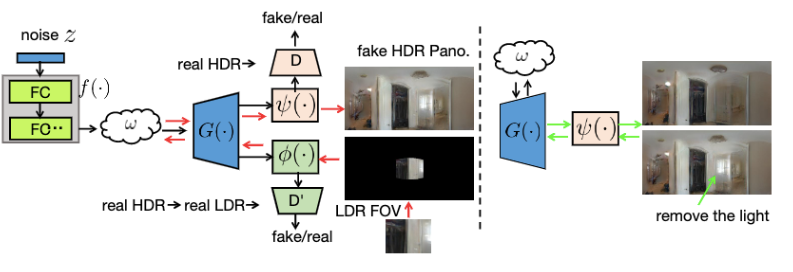
- 训练用的全景图GAN,然后LFOV到 LDR panoramas 用的 GAN inversion
2023-05-09 16:07:38
169
0
0
HiMODE: A Hybrid Monocular Omnidirectional Depth Estimation Model
- 室内全景图深度估计。似乎没有用到什么针对全景图的网络结构。
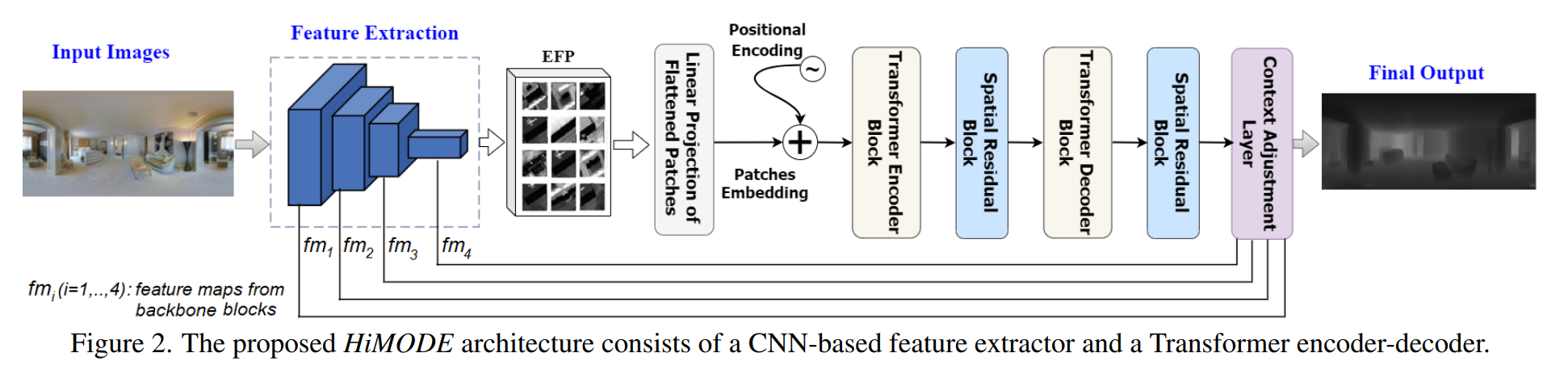
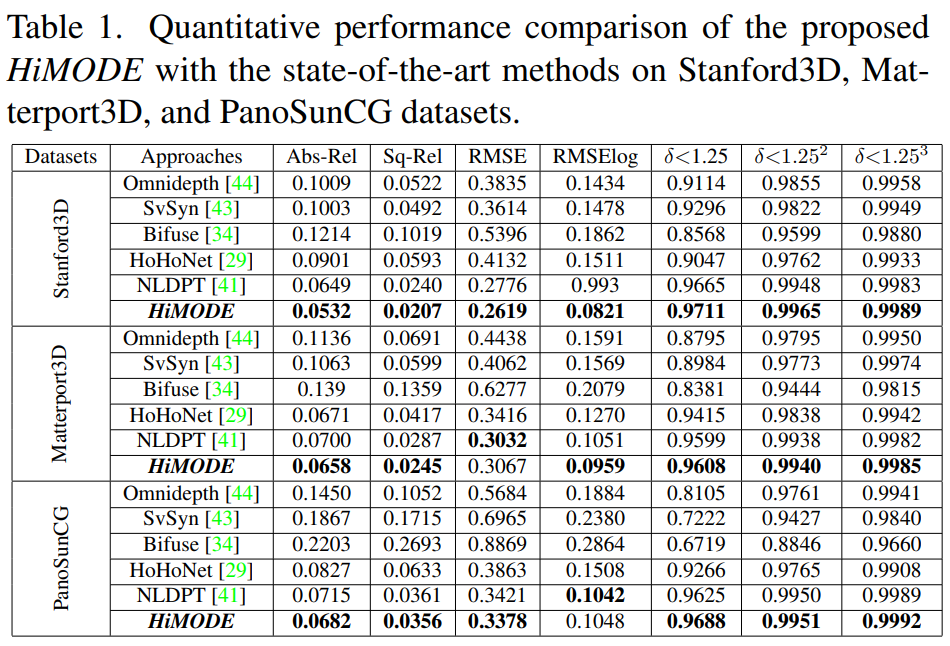
- 他说是ST3D 的 SOTA 那就是吧
其他
- Generative Scene Synthesis via Incremental View Inpainting using RGBD Diffusion Models: 用的是 ScanNetV2 (1.4T RGBD数据)。
- NYU-Depth V2: 室内RGBD数据,大约2.8G有语义标注,其余400GB只有深度。
- KITTI Eigen Split: KITTI的子集,大约30GB的样子。
- NeRDi: 用的是 Dense Prediction Transformer (DPT) model (一种密集预测的ViT,来自论文Vision Transformers for Dense Prediction),在一个共有 1.4M 张图的混合数据集上训练的(包括DIW,ETH3D,Sintel,KITTI,NYU,TUM)。有开源模型存档点。
- NeuralWindow Fully-connected CRFs for Monocular Depth Estimation: 上一篇的后续follow,没有混合数据集训练,但有NYUv2和KITTI的存档点。
- BinsFormer: 同样是后续SOTA之一。
- OmniFusion (CVPR2022) : 全景图单目深度估计。
- Monocular-Depth-Estimation-Toolbox: github 开源单目估计工具箱,支持四种SOTA模型,7种训练方法,4个主流数据集。劳模!
DAG: Depth-Aware Guidance with Denoising Diffusion Probabilistic Models
- CVPR2023 文章,代码暂时还没开源。
- 一个与深度密切相关的2D生成模型。
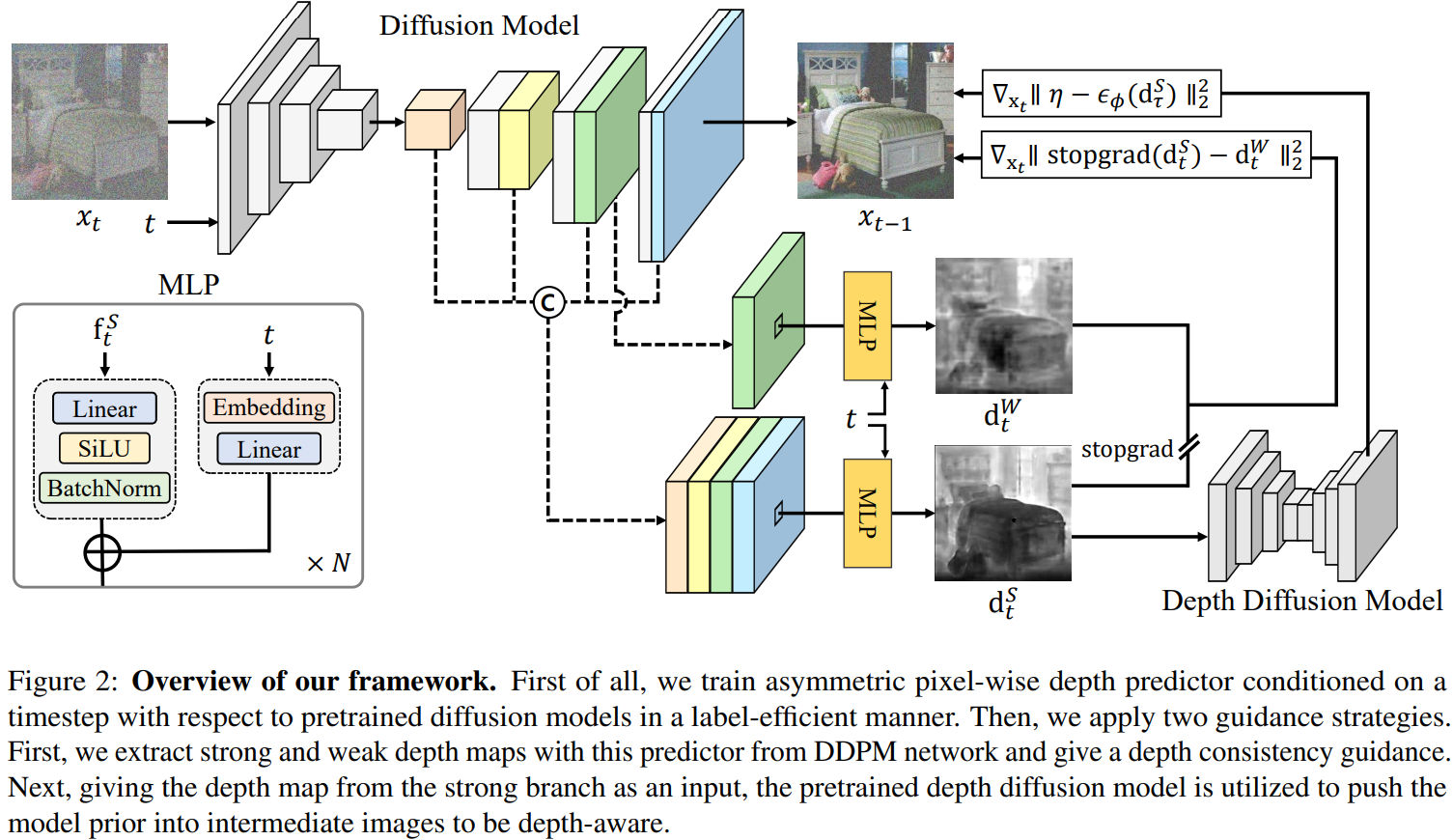
- 似乎质量还不错

2023-04-23 19:33:17
1129
0
0
Training-Free Layout Control with Cross-Attention Guidance
- 方法还是老一套,就是控制Cross-Attention,但是使用的是b
2023-04-22 19:12:46
168
0
0
总结
- 新的处理无界场景的思路——有限体素+NN decoder。
- 新的三维体积生成思路——先多视角RGBD+语义映射,再可微渲染微调改进。
GeNVS: Generative Novel View Synthesis with 3D-Aware Diffusion Models
- 效果很惊艳,但限制很大

- 就是训练了一个带条件的去噪模
2023-03-02 15:57:10
155
0
0
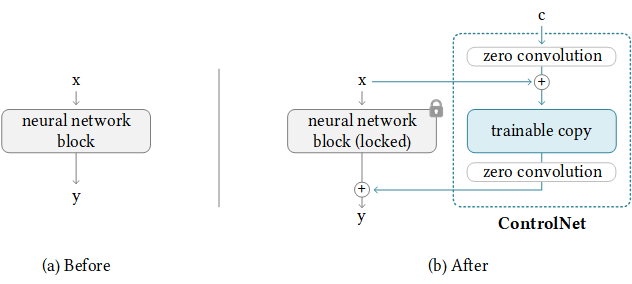
ControlNet
- 全新的架构思路,极好的效果和较低的训练开销。
- 任务目标,使用图片去控制diffusion的精准生成,效果极好,将SD的可控性提升了相当大的尺度。
- 最重要的几个trick:
- zero convolution,初始权重和bias都是0的卷积,可以保证作为额外的参数初始的时候,不会破坏原有网络inference的结果,也就是初始化在一个合理的位置,以及梯度不为0是可以训练的。
- trainable copy. 把原有网络复制一遍,然后配合 zero convolution 进行训练。
- jointly optimization. 数据集非常大时,可以使用大规模训练,也就是先训练好额外的部分,然后把锁定的权重解锁来联合优化。
2023-01-29 10:24:57
369
0
0
短期
- 短期主要方式为向Mesh兼容。主要体现形式为求解NeRF表征对应的最接近的Mesh表征,Mesh表征为基于三角网格与PBS材质的表征形式。Mesh转换分为两部分,第一部分为形状转换,第二部分为材质转换。
- 形状转换部分目前有基于 Marching Cube的直接转换和先拟合SDF再Marching Cube转换的方式。直接marching cube 转换的方式由于 NeRF 本身表面部分收敛结果较为不平整,所以通常结果可用用`灾难'形容。先拟合SDF再转Mesh的方式得到表面相对平滑可接受,目前主要代表为 NeuS 和 Instant-NSR。但使用marching cube 算法得到的Mesh 在应用中最常见的问题是表面太多了,相当于一个正常平面被强行切成很多网格小面,而且表面分布非常混乱。
- 材质转换部分目前研究工作较多,例如开源框架Pytorch3D 就非常简易的实现该功能。nvidia 的 NVDiffrast 也提供了相当便捷的Pytorch/Tensorflow 库和良好的硬件支持。
- 特别的 NVDiffrec 把这两者都完成了。值得一提的是 Tiny CUDANN 提供了非常广泛的隐式表征加速。
长期
- 长期方向应该是直接使用 NeRF 渲染。但主要问题是无法编辑、硬件支持性低、渲染开销高。
- 在快速渲染方面,mobile-nerf 已经实现了小模型手机端60fps的渲染,更多的硬件支持还比较缺乏。
- 在编辑方面只能说勉强实现了编辑,编辑便捷性和软件支持远不如Mesh,但编辑结果离真实结果还有差距。比如两个物体放在一起,很难把物体和物体之间的光效果体现出来(镜面反射、漫反射)。
2023-01-07 21:27:00
377
0
0
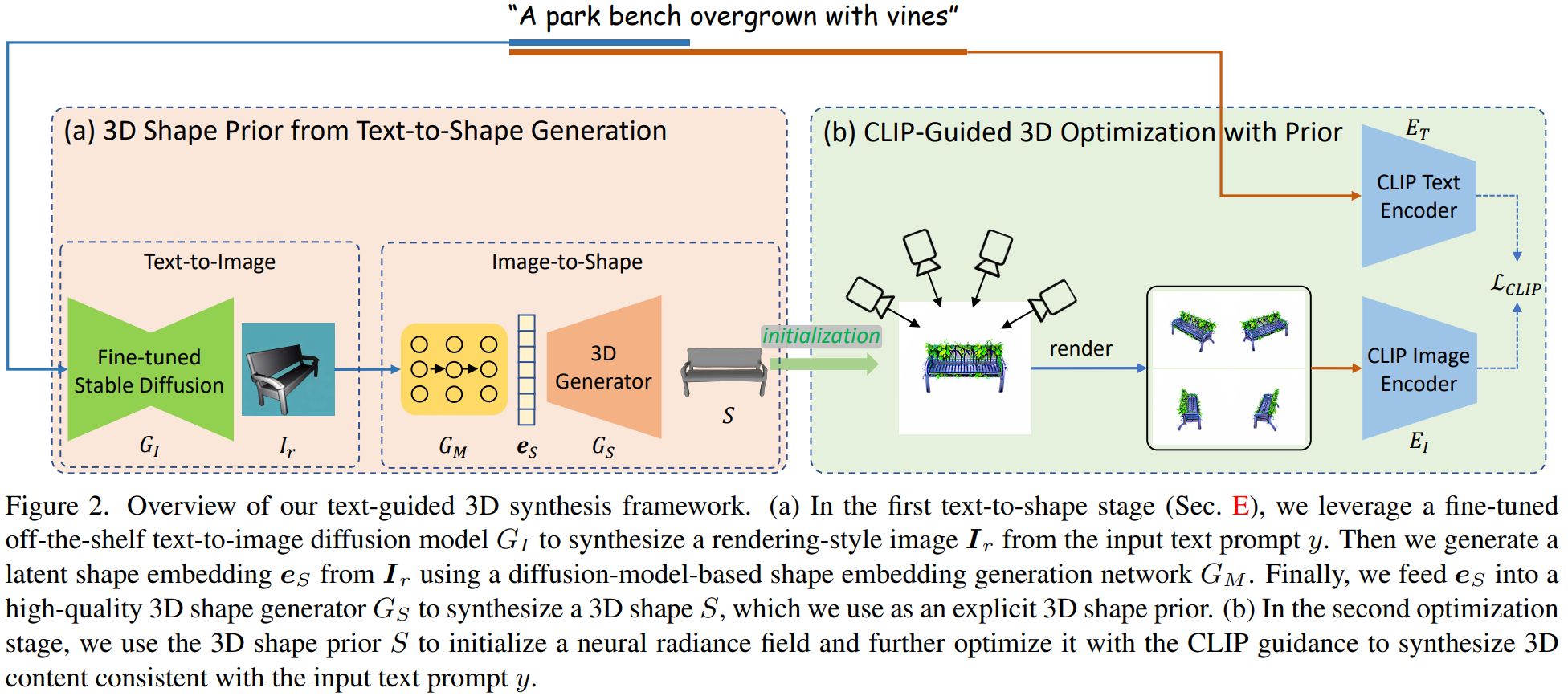
Dream3D: Zero-Shot Text-to-3D Synthesis Using 3D Shape Prior and Text-to-Image Diffusion Models
- 2D数据训练3D生成的方法。
- 先生成了形状,再进行染色。染色效果弱于现有工作,但是模型精细度更高。
- 有种作者不知道SDSLoss的感觉。
Generative Scene Synthesis via Incremental View Inpainting using RGBD Diffusion Models
- 通过不停的 RGBD 补全来生成大场景。
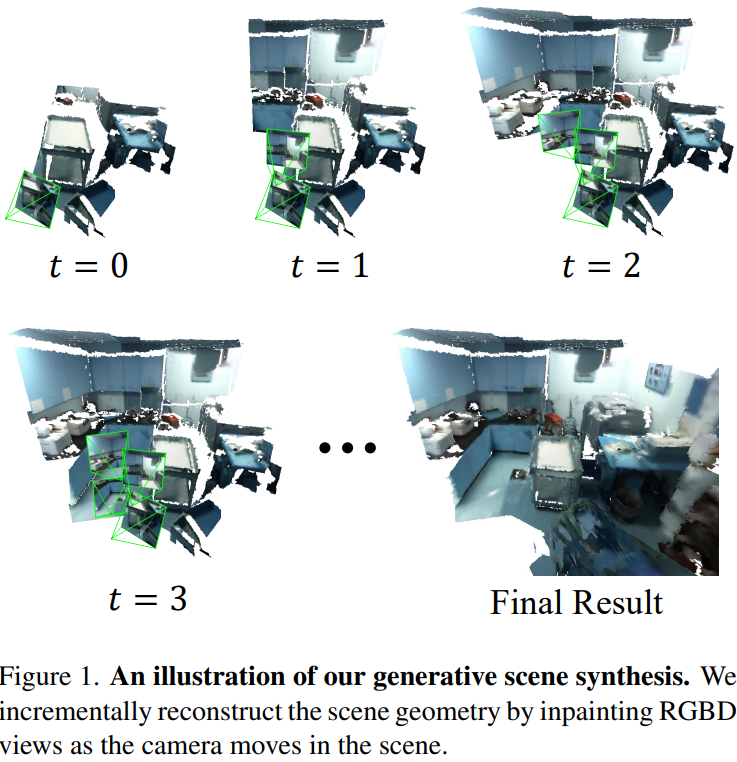
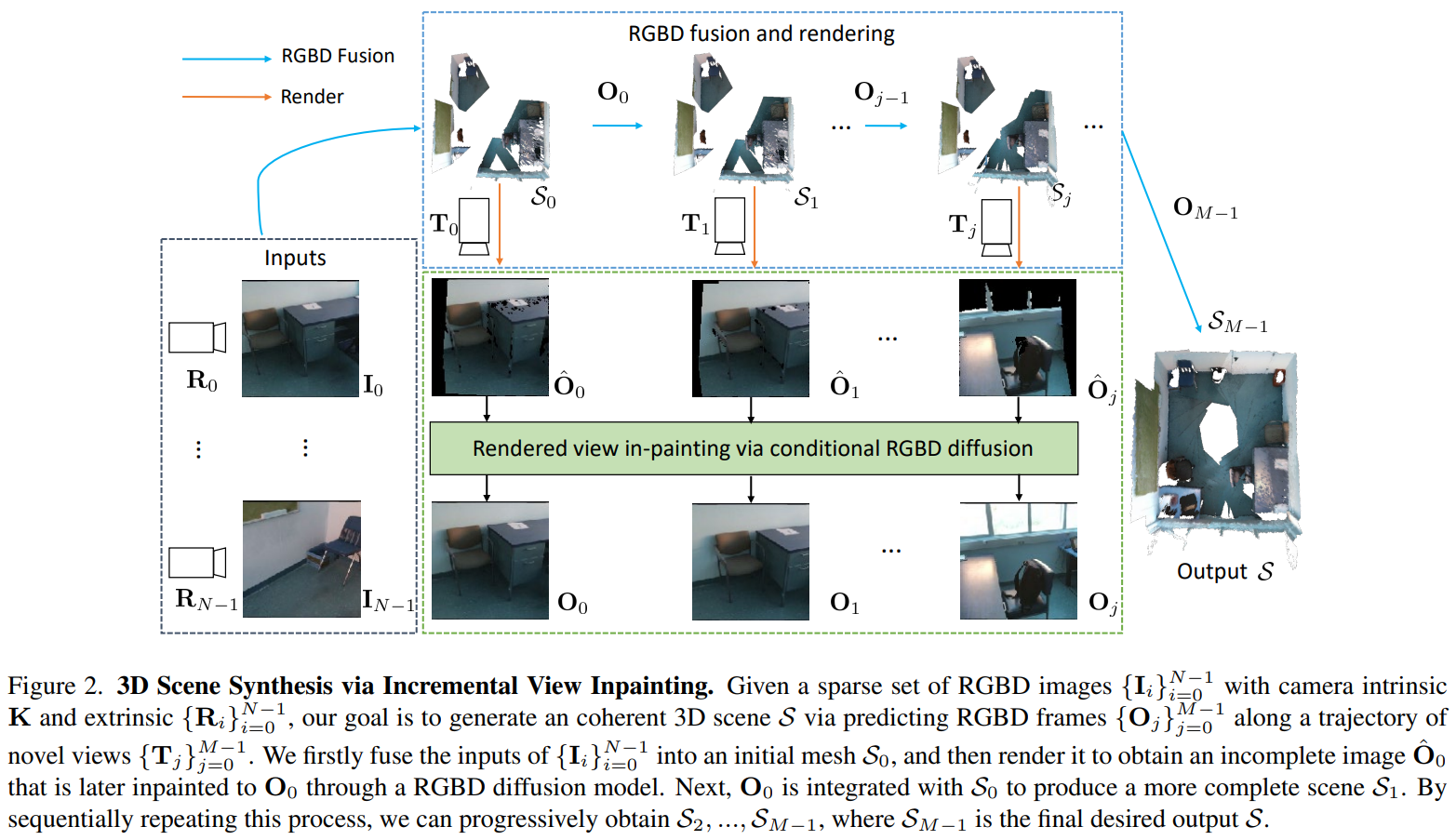
- 补全部分是个diffusion。
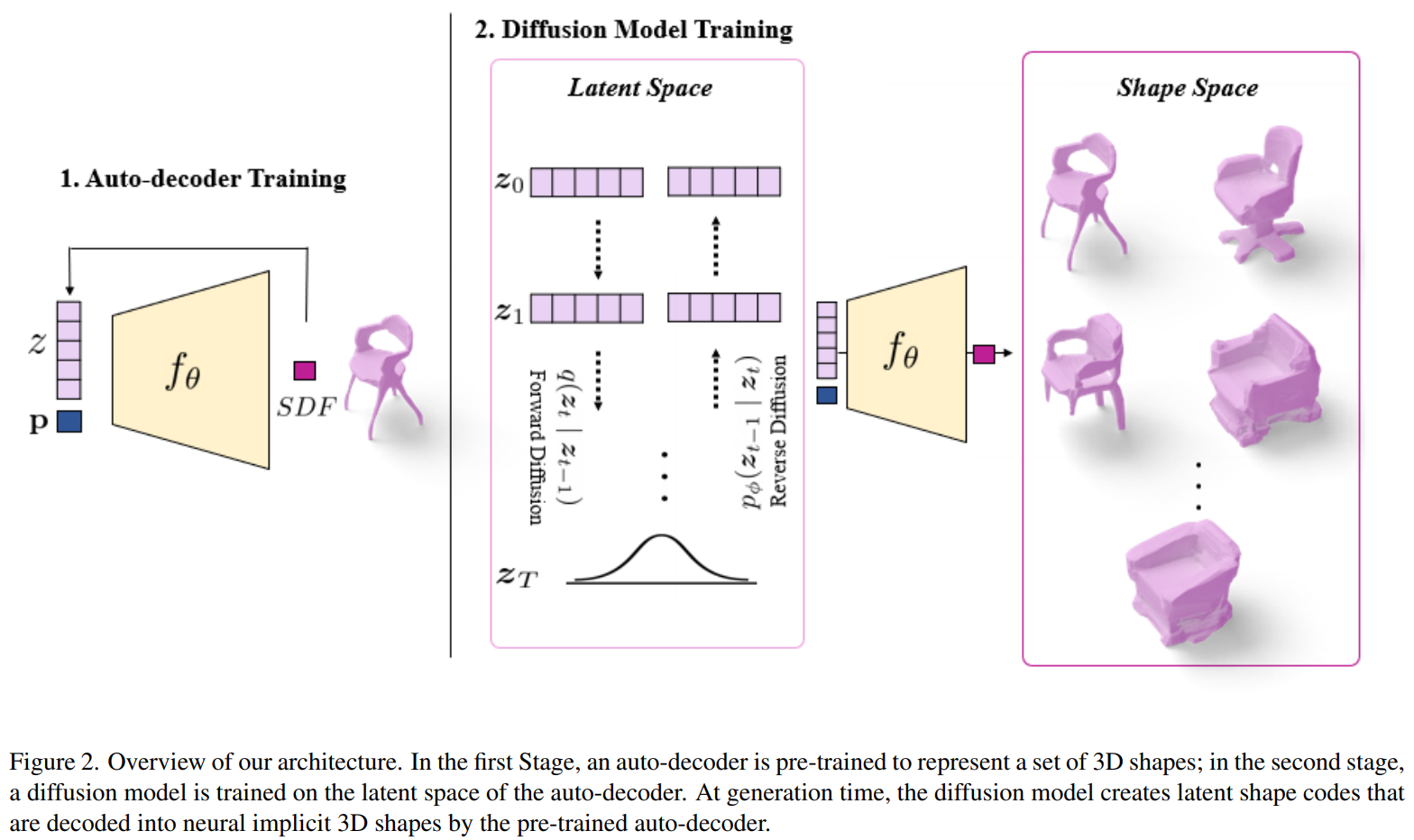
3D-LDM: Neural Implicit 3D Shape Generation with Latent Diffusion Models
- Latent Diffusion + SDF weight AE.

2022-12-30 10:56:43
235
0
0
- 多车协同
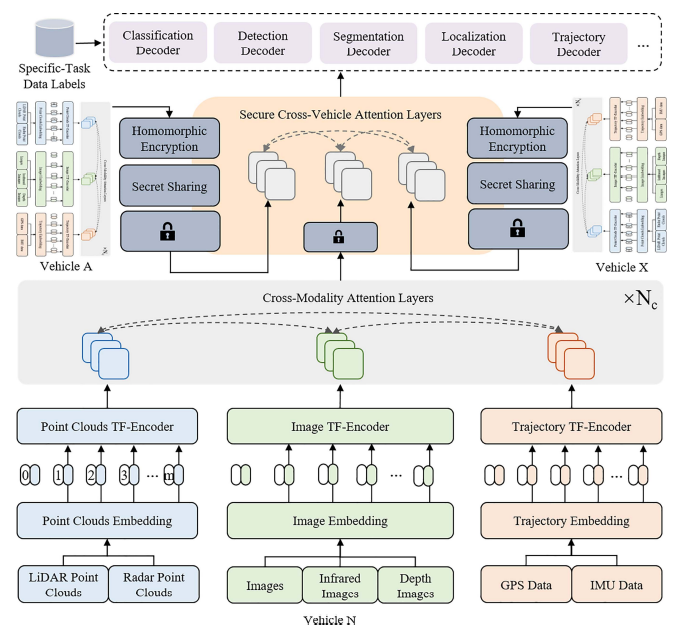
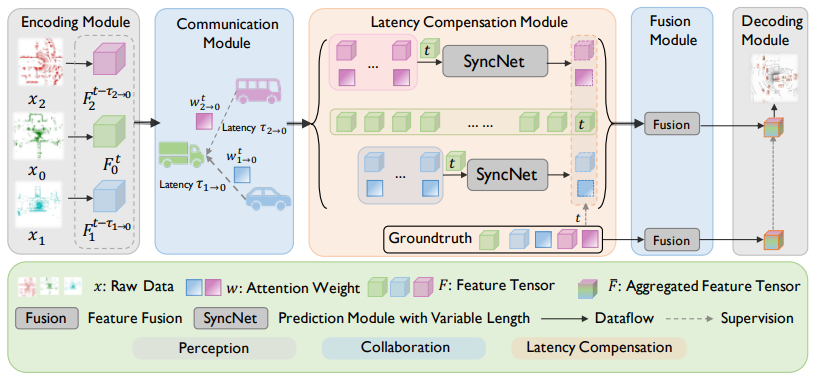
Latency-aware collaborative perception
- 联合感知
V2X-Sim: Multi-agent collaborative perception dataset and benchmark for autonomous driving
V2X-Sim: Multi-agent collaborative perception dataset and benchmark for autonomous driving
Object detection based on roadside LiDAR for cooperative driving automation: a review
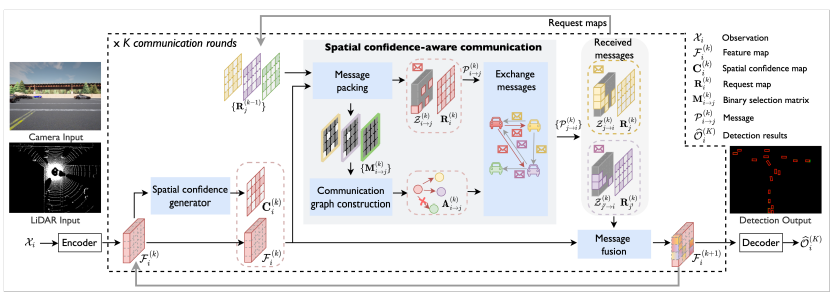
Where2comm: Communication-efficient collaborative perception via spatial confidence maps
- 车路协同,强调通信效率
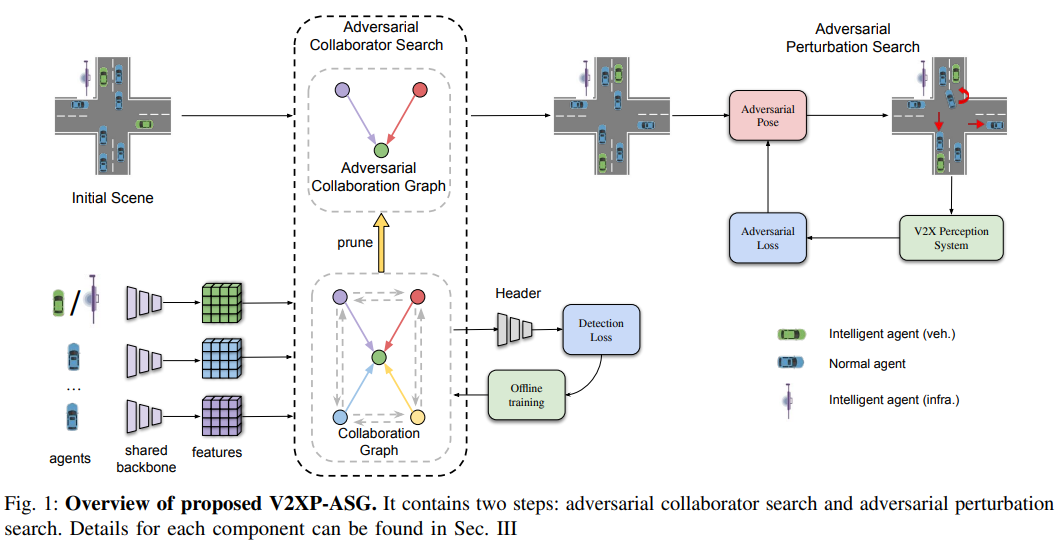
V2XP-ASG: Generating Adversarial Scenes for Vehicle-to-Everything Perception
- V2X
Object Detection Based on Roadside LiDAR for Cooperative Driving A
 wuvin
wuvin
