The recent rise of diffusion-based models

* 摘选翻译自 [The recent rise of diffusion-based models](https://maciejdomagala.github.io/generative_models/2022/06/06/The-recent-rise-of-diffusion-based-models.html).

# Introduction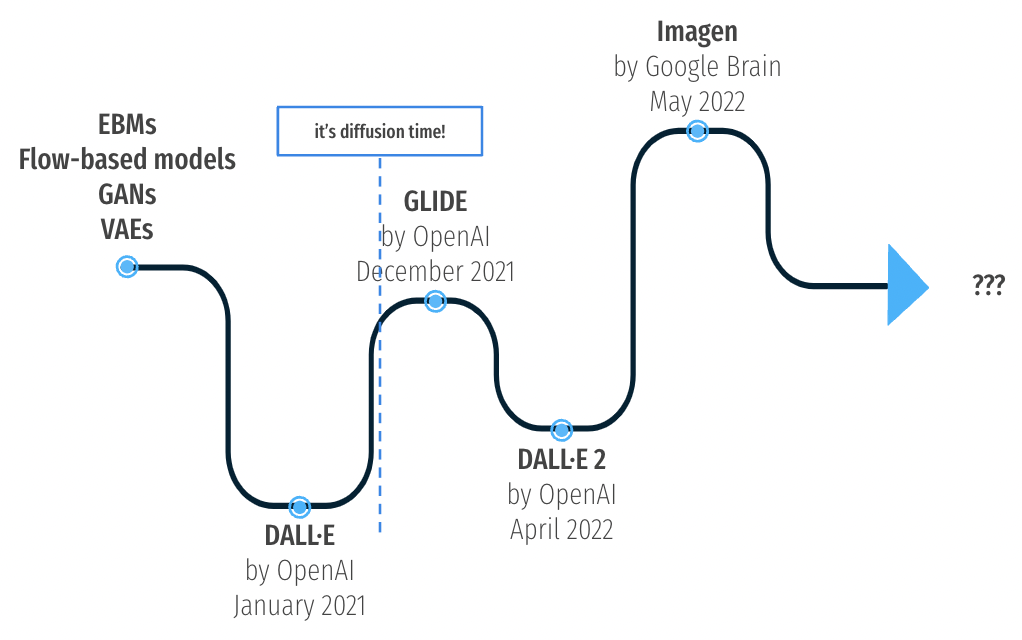

* ![title](https://leanote.com/api/file/getImage?fileId=63a27c06ab64411709a93dc0)
* 此处跳过对 DALLE 的VAE模型的回顾。
* 此处跳过对 CLIP 的回顾。

## All you need is diffusion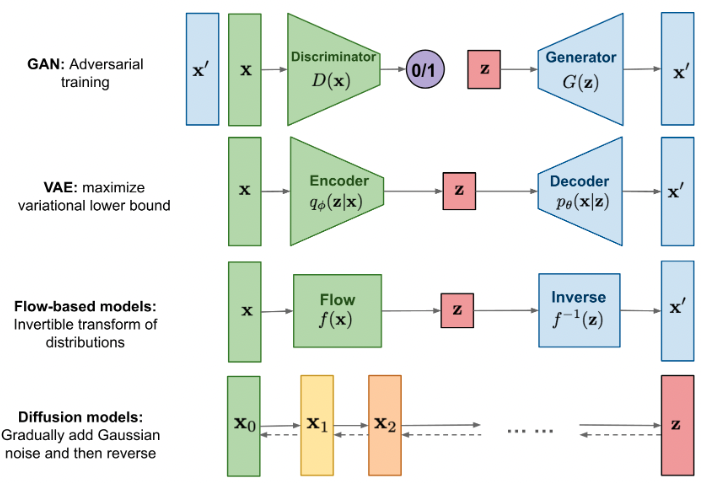

* ![title](https://leanote.com/api/file/getImage?fileId=63a27d60ab64411710a79050)
* 去噪模型是受热力学启发而来的，如下我们开始讲述去噪过程

### Forward image diffusion

* 首先对于去噪的每一步有个噪音规划 $\{\beta_{t}\}^{T}_{t=1}$, 那么前向扩散过程就是
$$q\left(\mathbf{x}_{t} \mid \mathbf{x}_{t-1}\right)=\mathcal{N}\left(\sqrt{1-\beta_{t}} \mathbf{x}_{t-1}, \beta_{t} \mathbf{I}\right).$$
* 随着噪音添加次数的增加，最终的 $q(\mathbf{x}_{T})$ 分布接近于高斯分布，这使得无论什么图像最终大家都会变成一个 $\epsilon \sim \mathcal{N}(0, \mathbf{I})$的分布。
* 并且可以直接推导出添加 $t$ 次噪音后的结果，而不需要逐步递推 
$$q\left(\mathbf{x}_{t} \mid \mathbf{x}_{0}\right)=\mathcal{N}\left(\sqrt{\bar{\alpha}_{t}} \mathbf{x}_{0},\left(1-\bar{\alpha}_{t}\right) \mathbf{I}\right) = \sqrt{\bar{\alpha}_{t}} \mathbf{x}_{0}+\sqrt{1-\bar{\alpha}_{t}} \cdot \epsilon,$$
其中 $\alpha_{t} := 1-\beta_{t}$, $\bar{\alpha}_{t} := \prod_{k=0}^{t}\alpha_{k}$, $\epsilon \sim \mathcal{N}(0, \mathbf{I})$.

### Reverse image diffusion

* 既然有了正向过程，只要让NN学习逆向过程就可以了。
* 逆向过程需要求解 $p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)=\mathcal{N}(\mu_{\theta}(\mathbf{x}_{t}, t), \Sigma_{\theta}(\mathbf{x}_{t}, t) ).$ 其中均值 $\mu_{\theta}(\mathbf{x}_{t}, t)$ 是NN预测的，方差 $\Sigma_{\theta}(\mathbf{x}_{t}, t)$ 则是根据噪音规划推到得到的，如 $\beta_{t}\mathbf{I}$。
* ![title](https://leanote.com/api/file/getImage?fileId=63a28453ab64411710a7908b)
* 去噪模型的训练阶段有如下步骤：
    * 采样一张图片 $\mathbf{x}_{0}\sim q(\bf{x}_{0})$.
    * 随机一个step $t \sim U(\{1,2,...,T\})$.
    * 添加噪音 $\epsilon \sim \mathcal{N}(0,\mathbf{I})$。
    * NN估计这个噪音 $\epsilon_{\theta}(\mathbf{x}_{t}, t)= \epsilon_{\theta}(\sqrt{\bar{\alpha}_{t}} \mathbf{x}_{0}+\sqrt{1-\bar{\alpha}_{t}} \cdot \epsilon, t)$.
    * 通过SGD优化NN从而降低损失函数 $ \|\epsilon - \epsilon_{\theta}(\mathbf{x}_{t}, t)\|^{2}$.
* 简单来说优化目标就是 $L_{\text{diffusion}}=\mathbb{E}_{t, \mathbf{x}_{0}, \epsilon}\left[\left\|\epsilon-\epsilon_{\theta}\left(\mathbf{x}_{t}, t\right)\right\|^{2}\right]$

### Guiding the diffusion

* 第一种加引导的方式是在有噪音的图像上预训练一个分类器判别种类，然后在去噪生成过程中添加分类loss的梯度使得分类结果更接近于我们期望的一类。
* 第二种引导方式则不需要额外的监督网络。在训练模型 $\epsilon_{\theta}(\mathbf{x}_{t}, t \mid y)$ 时有时候传入图片种类信息 $y$，有时候把 $y$ 替换为空 $\emptyset$。而预测的时候，则进行两次推理，一次使用 $\epsilon_{\theta}(\mathbf{x}_{t}, t \mid y)$，另一次使用 $\epsilon_{\theta}(\mathbf{x}_{t}, t \mid \emptyset)$，而最终的去噪结果则使用一个**大于一**的引导缩放$S$。
* $$\hat{\epsilon}_{\theta}\left(\mathbf{x}_{t}, t \mid y\right)=\epsilon_{\theta}\left(\mathbf{x}_{t}, t \mid \emptyset\right)+s \cdot\left(\epsilon_{\theta}\left(\mathbf{x}_{t}, t \mid y\right)-\epsilon_{\theta}\left(\mathbf{x}_{t}, t \mid \emptyset\right)\right)$$
* 这个方法被 [Nichol et al.](https://arxiv.org/pdf/2112.10741.pdf) 提出。
* 能这么做是因为 ![title](https://leanote.com/api/file/getImage?fileId=63a2c7e8ab64411709a94112)

## Text-guided diffusion with GLIDE

* 对于Text引导，我们最关心的是两个问题
    * 我们该如何使用Text引导信息？
    * 我们如何在使用引导信息的情况下保证高质量的生成？

### Architecture choice

* 架构上通常包含一下三部分：
    * 一个用于预测噪音的 U-net
    * 一个用于文字编码的 Transformer
    * 一个用于输出图像进一步超分的 Diffusion
* 在 DALL·E2 中，生成是基于CLIP Embedding 的，即给定 text-embedding 然后生成一个 CLIP-Embedding 用于给 CLIP-Image-Decoder。去噪过程是在隐空间中进行的。
* 并且 DALL·E2 改进了训练 Diffusion 的 Loss，由
* $$L_{\text{diffusion}}=\mathbb{E}_{t, \mathbf{x}_{0}, \epsilon}\left[\left\|\epsilon-\epsilon_{\theta}\left(\mathbf{x}_{t}, t\mid y\right)\right\|^{2}\right],$$ 改为
* $$L_{\text{prior:diffusion}}=\mathbb{E}_{t}\left[\left\|z_{i}-f_{\theta}\left({z}_{i}^{t}, t \mid y\right)\right\|^{2}\right],$$ 即直接预测样本本身。

wuvin

导航

最近发表

友情链接